نجات الگوریتم بازگشتی با Tail Call

الگوریتم بازگشتی جزو الگوریتم‌های خلاقانه‌ای محسوب می‌شه که گرچه شاید در ابتدا درکش کمی سخت باشه، اما وقتی که بهش عادت کنی، می‌بینی چقدر می‌تونه توی ساده‌تر شدن، خواناتر شدن و کوتاه‌تر شدن کد کمک کنه. با این حال انگلیسی‌ها ضرب‌المثلی دارن که می‌گه:

Everything comes with a price.

یا به عبارتی: هر چیزی بهایی داره. بهای این ساده‌تر و خواناتر و کوتاه‌تر شدن کد، مصرف حافظۀ زیاد و مرتبۀ زمانی نمایی در الگوریتم بازگشتی است. کافیه موقع پیاده‌سازی الگوریتم بازگشتی لحظه‌ای غفلت کنیم تا با خطای استک اورفلو مواجه بشیم. اما اصلاً چرا این الگوریتم‌ها مصرف حافظۀ بالایی دارند و آیا راهی وجود داره که بشه این مصرف رو کاهش بدیم؟ توی این مطلب می‌خوایم این موضوع رو بررسی کنیم و در انتها هم نگاهی به رویکرد زبان Go در قبال این موضوع بندازیم.

سرفصل‌های این مطلب:

• چرا مصرف حافظۀ الگوریتم بازگشتی بالاست؟
• معجزه با واپسین درخواست!
• گولنگ و Tail Call Optimization

چرا مصرف حافظۀ الگوریتم بازگشتی بالاست؟

برای جواب به این سوال، اول لازمه بدونیم که یک برنامه چطور اجرا می‌شه.

زمانی که برنامه‌ای رو می‌نویسیم و سپس کامپایل می‌کنیم، کامپایلر اون رو تبدیل به کدهای ماشینیِ خوانا برای دستگاه‌های کامپیوتری می‌کنه. وقتی برنامه رو اجرا می‌کنیم، این کدهای ماشینی در بخشی از RAM بارگذاری می‌شن و دستگاهمون هم از تابع اصلی برنامه‌مون شروع می‌کنه، گام به گام از روی اون کدها پیش می‌ره و دستورات رو اجرا می‌کنه. بیشتر اوقات اجرای این دستورات گام‌به‌گام و پشتِ سرِ هم اتفاق می‌افته. گاهی هم ممکنه یک سری از دستورات رو رد کنه یا چند بار تکرار کنه (مثلاً اون بخش‌هایی که از IF یا حلقه‌ها استفاده کردیم). یک حالت دیگه هم وجود داره که ممکنه این اجرای خط‌به‌خط دچار تغییراتی بشه. اونم وقتیه که ما داخل برنامه‌مون تابع دیگه‌ای رو فراخوانی کردیم.

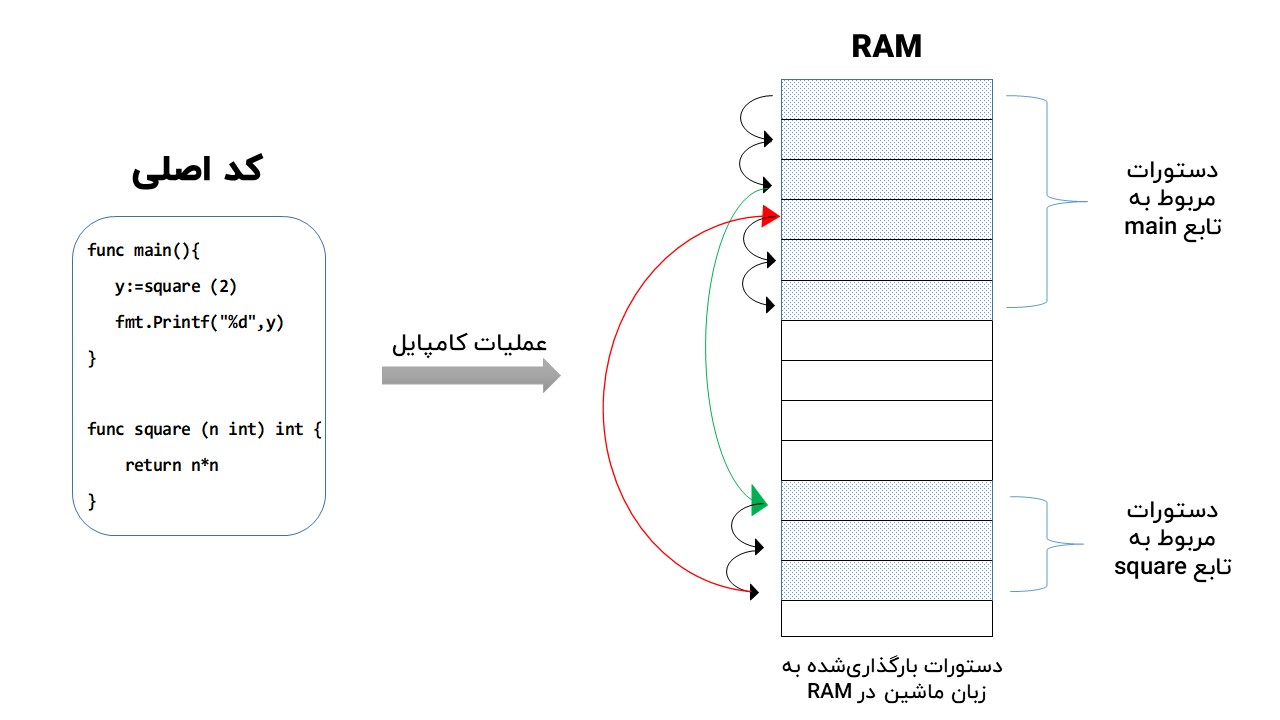
تابع فرعی که فراخوانیش کردیم، مثل تابع اصلی که در حال اجراست، یک تکه‌کده که کامپایلر اون رو هم به کدهای ماشینی تبدیل کرده و وقتی که فراخوانیش می‌کنیم، اون کدها رو در بخش دیگری از RAM بارگذاری و شروع به اجرای دستوراتش می‌کنه. پس اینجوری تصور کنین: داریم در تابع اصلی برنامه‌مون پیش می‌ریم و ناگهان تابع دیگه‌ای رو فراخوانی می‌کنیم که اطلاعاتش در بخش و آدرس دیگه‌ای از حافظه ذخیره شده. دستگاه به اون آدرس می‌ره که دستورات تابع فرعی رو اجرا کنه (فلش سبز در تصویر بالا).

تا اینجا که مشکلی نیست. اما موضوع اینجاست که بعد از اتمام اجرای تابع فرعی، لازمه که به تابع اصلی برگردیم و اجرای بقیۀ خطوط کدِ تابع اصلی رو از سر بگیریم. در اصطلاح به این کار می‌گیم return کردن (فلش قرمز در تصویر قبل). اما برای این کار باید بدونیم کدهای تابع اصلی در چه آدرسی از حافظه ذخیره شده‌اند. پس هر بار که یک تابع فرعی فراخوانی می‌شه، قبل از اینکه سراغ کدهای تابع فرعی بریم، باید آدرس کدهای تابع اصلی رو همراه با تمام متغیرهای در حال استفاده در تابع اصلی، جایی ذخیره کنیم که بعد از اتمام کار با تابع فرعی بتونیم بهشون برگردیم. به‌صورت ساده فرض کنید مجموعۀ این اطلاعات رو در یک واحد ذخیره‌سازی می‌کنیم که بهش Frame می‌گیم. در نتیجه موقع فراخوانی یک تابع فرعی، یک فریم مربوط به تابع اصلیه و فریم بعدی مربوط به تابع فرعی که حاوی آدرس کد و متغیرهای تابع فرعیه.

وقتی کار تابع فرعی تموم می‌شه و به تابع اصلی برمی‌گردیم، کارمون با فریم تابع فرعی هم تموم می‌شه و می‌تونیم اون بخش از حافظه رو که بهش اختصاص دادیم دور بندازیم و حافظه رو آزاد کنیم. زمانی هم که تابع اصلی به پایان کارش می‌رسه، کارمون با فریم تابع اصلی تموم می‌شه، برنامه به پایان می‌رسه و اون بخش از حافظه هم آزاد می‌شه.

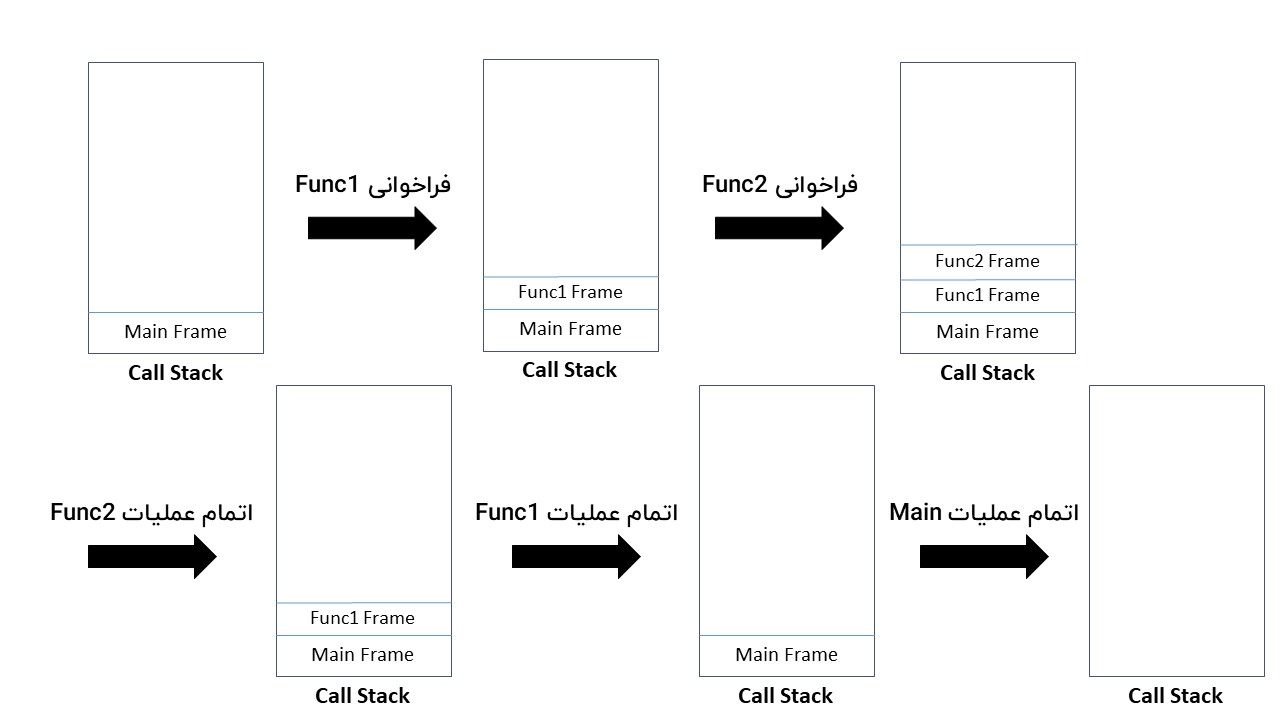
حالا بیاین تصور کنیم که تابع فرعی ما داخل خودش یک تابع فرعی دیگه رو فراخوانی کنه… همۀ این روند باید تکرار بشه. یعنی یک فریم دیگه برای اطلاعات تابع فرعی 2 ایجاد بشه که اطلاعات مربوط به اون تابع داخلش ذخیره شده باشه. در نتیجه حالا سه تا فریم داریم: فریم مربوط به تابع فرعی 2، فریم مربوط به تابع فرعی 1 و فریم مربوط به تابع اصلی. وقتی کار تابع فرعی 2 تموم بشه و به تابع فرعی 1 برگردیم، فریمش هم حذف می‌شه و همین اتفاق برای فریم تابع فرعی 1 در زمان برگشت به تابع اصلی می‌افته.

با توجه به نحوۀ عملکرد فریم‌ها، برای پیاده‌سازی‌شون از ساختار پشته (Stack) استفاده شده و آخرین عضوی که وارد پشته می‌شه، اولین عضویه که خارج می‌شه (Last In First Out). به این پشته که فریم‌ها داخلش ذخیره می‌شه Call Stack می‌گن.

حالا بیاین ببینیم توی الگوریتم‌های برگشتی چه اتفاقی می‌افته. برای نمونه کد زیر فاکتوریل عدد n رو به روش بازگشتی محاسبه می‌کنه:

func Factorial(n int64) int64 {
      if n == 1 {
      return 1
}
      return n * Factorial(n-1)
}

این تابع توی هر بار اجرا، یک بار دیگه خودش رو فراخوانی می‌کنه که یعنی یک فریم جدید به Call Stack اضافه می‌شه و در نتیجه با هر بار فراخوانی، بخش بیشتری از حافظه رو اشغال می‌کنیم. هیچ‌کدوم از اون فریم‌های میانی رو نمی‌تونیم دور بندازیم، چون در اون صورت راه برگشت به تابع اصلی گم می‌شه. ضمن اینکه برای محاسبۀ نتیجۀ نهایی، لازمه که به آخرین گام (Base Case) برسیم، توابع یکی پس از دیگری return کنند، فریم‌هاشون از کال استک حذف بشه و در نهایت قبل از return نهایی، فاکتوریل رو حساب کنیم و بعد با نتیجه به تابعی برگردیم که تابع Factorial رو صدا زده.

علت مصرف بالای حافظۀ الگوریتم‌های بازگشتی، همین تلنبار شدن فریم‌های توابع میانیِ فراخوانی‌شده است. حتماً با سایت StackOverflow آشنا هستین. اسم این سایت از یک خطای شوم در اجرای برنامه‌های کامپیوتری گرفته شده که با توضیحات بالا احتمالاً می‌تونین حدس بزنید چه زمانی رخ می‌ده. هر Call Stack محدودیت حافظه‌ای خاصی داره و اگر تعداد فریم‌هایی که قراره داخلش ذخیره بشه از اون محدودیت فراتر بره، سرریز می‌کنه (Overflow) و با خطای Stack Overflow مواجه می‌شیم. خطایی که هنگام استفاده از الگوریتم‌های بازگشتی همیشه در کمین ماست.

معجزه با واپسین درخواست!

آیا راهی هست که بشه توی الگوریتم‌های بازگشتی، فریم‌های میانی رو حذف کرد؟

در الگوریتم بازگشتی اگر الگوریتم رو به گونه‌ای پیاده کنیم که بعد از رسیدن به آخرین گام، برای محاسبۀ جواب مد نظرمون مجبور نباشیم تا اولین تابع فراخوانی‌شده برگردیم، می‌تونیم به قیمت دشوارتر کردن فرایند دیباگ، فریم‌های میانی رو حذف کنیم. بذارید برای روشن‌تر شدن منظور، به مثال فاکتوریل برگردیم.

توی تکه‌کدی که آخر بخش قبل آورده شد، دیدیم که برای محاسبۀ فاکتوریل حتماً باید به Base Case برسیم و سپس تا اولین تابع فراخوانی‌شده برگردیم و بعد فاکتوریل رو محاسبه کنیم. در واقع موقع رسیدن به Base Case، حتی اگر آدرسِ محل ذخیره‌سازی کد تابع اصلی رو داشته باشیم، نمی‌تونیم به اون برگردیم، چون هنوز نمی‌دونیم جواب مسئله‌مون چی می‌شه! حالا کد زیر رو ببینین:

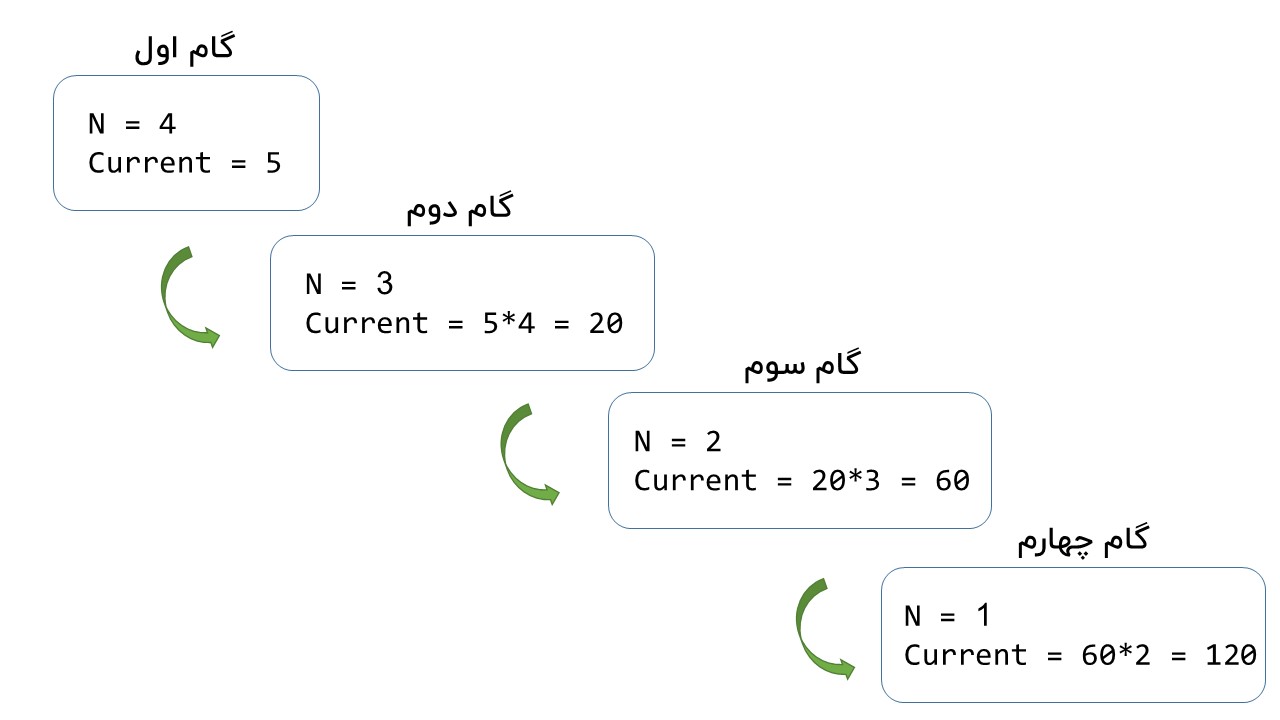
func factorialN(n, current int64) int64 {
      if n == 1 {
      return current
}
      return factorialN(n-1, n*current)
}
func TailRecursionFactorial(n int64) int64 {
      return factorialN(n-1, n)
}

توی این کد برای محاسبۀ فاکتوریل از یک تابع کمکی استفاده کردیم و صرفاً کافیه تابع TailRecursionFactorial رو فراخوانی کنیم. اما استفاده از این تابع کمکی باعث ایجاد تفاوت مهمی با کد قبلی شده: در این کد وقتی به Base Case می‌رسیم، جواب نهایی رو داریم و برای محاسبه‌اش مجبور نیستیم به اولین تابع فراخوانی‌شده برگردیم. تصویر زیر، گام‌های محاسبۀ فاکتوریل 5 رو بر اساس کد بالا نشون می‌ده. همون‌طور که مشاهده می‌کنید، وقتی به Base Case می‌رسیم (که در این کد n == 1 است)، مقدار نهایی فاکتوریل رو داریم و به‌نوعی می‌شه گفت دیگه نیازی به برگشت به اولین فراخوانی تابع نداریم.

حالا اگر کامپایلر بتونه تشخیص بده توی الگوریتمی که ما نوشتیم نیازی به فریم‌های میانی بعد از پایان اجرای تابع مربوطه‌شون نیست، می‌تونه بعد از پایان هر تابع و پاس دادن مقادیر لازم به تابع بعدی، از شر اون فریم خلاص بشه و در نتیجه مشکل استک اورفلوی احتمالی حل می‌شه.

برای اینکه کامپایلر بتونه چنین تشخیصی بده و کلاً چنین کاری امکان‌پذیر باشه، در اصطلاح باید فراخوانی تابع بازگشتی‌مون در موقعیت Tail Call رخ بده. من معادلش رو گذاشتم واپسین درخواست، چون وقتی می‌گیم فراخوانی تابعی در موقعیت Tail Call قرار داره که اون فراخوانی، آخرین کار تابع قبل از به پایان رسیدنش باشه. پس اگر واپسین درخواست تابع ما اجرای دوبارۀ خودش باشه، می‌شه اون الگوریتم رو بهینه کرد (چون می‌دونیم این آخرین کاریه که می‌کنه و در نتیجه دیگه نیازی به اطلاعات فریمش نیست). به این کار می‌گن Tail Call Optimization یا اگر با ترجمۀ خودمون پیش بریم می‌شه بهش گفت بهینه‌سازی واپسین درخواست.

نکته: در الگوریتم اول، آخرین درخواستی که تابع فاکتوریل داشت، محاسبۀ ضرب n در حاصل تابع بازگشتی بود و نه فراخوانی تابع بازگشتی. در نتیجه نمی‌شد اون تابع رو بهینه‌سازی کرد.

مهم‌ترین موضوع توی TCO اینه که کامپایلر شما توانایی تشخیص واپسین درخواست رو داشته باشه و بعد از تشخیص بر اون اساس بهینه‌سازی رو اعمال کنه. بعضی زبان‌ها و بعضی کامپایلرها، توجهی به این موضوع ندارن. در نتیجه هر چقدر هم الگوریتم‌هاتون رو جوری بنویسید که فراخوانی تابع بازگشتی در موقعیت Tail Call اتفاق بیفته، چون کامپایلر توجهی به این موضوع نداره، از نظر مصرف حافظه هیچ بهبودی در عملکرد مشاهده نمی‌کنید.

یکی از زبان‌هایی که توجهی به TCO نداره، گولنگه. اما چرا؟ و آیا می‌شه با وجود این عدم پشتیبانی، بدون نگرانی از رخ دادن استک اورفلو، با گولنگ الگوریتم بازگشتی پیاده‌سازی کرد؟

پیش از رفتن به بخش بعد: تا اینجا دیدیم که الگوریتم‌های بازگشتی چه مشکلاتی دارند، واپسین درخواست یا Tail Call چیه و چطور می‌تونه در بهینه‌سازی مصرف حافظۀ این الگوریتم‌ها کمک کنه. حالا می‌خوام توصیه کنم که این ویدیو رو تماشا کنین. ارائه‌ای دونفره در کنفرانس Con 2019!! که این دو خانم کل مبحث TCO رو به‌شکل بسیار جذاب و خلاقانه‌ای تبدیل به ترانه کردند و اجرا می‌کنند. خودم خیلی از خلاقیت و شیوۀ ارائه‌شون لذت بردم و انتهای اجرا واقعاً پای مانیتور براشون دست زدم. به‌نظرم از دستش ندید.

گولنگ و Tail Call Optimization 

همون‌طور که گفتیم توی TCO فریم‌های میانی دور ریخته می‌شن و طبق همون ضرب‌المثلی که اول مطلب بهش اشاره کردیم، هر چیزی بهایی داره. بهای TCO اینه که دیباگ کردن به‌شدت سخت می‌شه، چون اگر خطایی در نتیجۀ نهایی وجود داشته باشه، به فریم‌های میانی دسترسی نداریم. گولنگ ترجیح داده این بها رو نپردازه، به همین دلیل کامپایلر گو واپسین درخواست‌ها رو بهینه نمی‌کنه. شما چه الگوریتم بازگشتی خودتون رو طوری پیاده کنین که فراخوانی مجدد تابع در موقعیت Tail Call رخ بده چه نه، در نهایت احتمالاً با خطای استک اورفلو مواجه می‌شین. به همین دلیله که توی گولنگ استفاده از الگوریتم بازگشتی کار حساس و احتمالاً نابهینه‌ایه. از طرفی تقریباً هرکاری که با الگوریتم بازگشتی انجام‌پذیره، با حلقه‌ها و تکرار (Iteration) هم امکان‌پذیره و در گو بهتره که سراغ استفاده از حلقه‌ها بریم.

اما می‌خوام هر جور شده با گو الگوریتم بازگشتی بنویسم و به استک اورفلو نخورم! یعنی می‌گی نمی‌شه؟

یک راه میانبر وجود داره که اصلاً بهینه نیست، کُنده و منابع زیادی از دستگاهتون مصرف می‌کنه، اما شما رو با خطای استک اورفلو مواجه نمی‌کنه: استفاده از گوروتین و کانال‌.

کد زیر رو که برای محاسبۀ فاکتوریل با این روش پیاده‌سازی شده ببینید:

func main() {
      result := make(chan int64)

      recursiveChannel(n, 1, result)
      answer := <-result
      fmt.Printf("Result is: %d", result)
}

func channelFactorial(n, current int64, result chan int64) {
      if n == 1 {
      result <- current
      return
}
      go channelFactorial(n-1, n*current, result)
}

کانسپت اصلی شبیه Tail Call است، اما با این تفاوت که تابع بازگشتی ما هیچ چیزی رو برنمی‌گردونه، بلکه در آخرین گام و قبل از return کردن، در یک گوروتین، دوباره خودش رو فراخوانی می‌کنه. طبق اصول همزمانی در گو، تابع ما منتظر اجرای کامل گوروتین نمی‌شه و به پایان خودش می‌رسه و return می‌کنه و Garbage Collector گو نیز فریم حافظۀ اختصاص داده شده به اون رو پاک می‌کنه. اما گوروتینی که فراخوانی کردیم به حیات خودش ادامه می‌ده و پیش از اینکه خودش به پایان کار برسه، گوروتین دیگه‌ای رو فراخوانی می‌کنه و این روند اون‌قدر ادامه پیدا می‌کنه که به Base Case برسیم. زمانی که به Base Case رسیدیم، فقط یک گوروتین فعال وجود داره که اون هم نتیجه رو داخل کانالی می‌ریزه که از ابتدا تعریف کرده بودیم.

تابع main بعد از اولین فراخوانی تابع بازگشتی ما، منتظر ریخته شدن چیزی توی اون کاناله و جلوتر نرفته. به محض اینکه چیزی وارد کانال می‌شه، اون مقدار رو می‌گیره و اجرای بقیۀ خطوطش رو ادامه می‌ده. به این ترتیب می‌شه مشکل استک اورفلو رو حذف کرد، چون دیگه فریم‌ها روی هم تلنبار نمی‌شن، اما در مجموع روش بسیار نابهینه‌ایه و توی گولنگ همچنان توصیه می‌شه هر جا امکانش هست، از تکرار استفاده کنیم، نه از بازگشت.

منابعی که برای نوشتن این مطلب استفاده شدند:

• Recursion and Tail Calls in Go –  Gopher Academy Blog
• Tail Call Optimization – 0612 TV w/ NERDfirst
• Tail Recursion Explained – Computerphile
• !!Con 2019- Tail Call Optimization: The Musical!! by Anjana Vakil & Natalia Margolis